Essai de datation des nefs à trois vaisseaux : les méthodes, page d'annexes 

• Essais de datation    • Article précédent    • Article suivant


La présente page est une page d'annexes dont le but est d'apporter des précisions sur les méthodes appliquées dans la page précédente, afin de ne pas alourdir cette dernière. Le lecteur qui ne souhaite pas prendre connaissance de ces précisions peut passer directement à la page suivante.



Annexe 1 concernant la première apporoche de l'étape 1 : Évaluation en pourcentage de l'effectif des monuments attribuables au premier millénaire de notre ère.

Elle consiste à déterminer le taux d'accroissement de la population européenne durant le premier millénaire, en s'inspirant des données statistiques concernant la population mondiale trouvées sur Internet. Voici quelques-unes de ces données.

Sur le site Internet Wikipédia, on dispose des données suivants, en millions d'habitants :

en l'an -5000 : 5 à 20.

en 400 : 190 à 206.

en 1000 : 254 à 345.

en 1250 : 400 à 416.

en 1500 : 425 à 540.

en 1700 : 629 à 691.


Les renseignements sont répartis dans le tableau suivant :



  • Modèle avec le taux de 8,673.

    Tableau 1
    Modèle avec le taux de 8,673.

La première des lignes recense les siècles, du premier au dix-septième. La deuxième ligne est l'estimation de la valeur inféreure de la population mondiale au siècle correspondant. La troisième ligne, de la valeur supérieure. La quatrième, de la valeur moyenne entre les deux précédentes. Enfin, la cinquième ligne est obtenue en prenant un taux d'accroissement de 8,67 % par siècle. On obtient le graphe ci-dessous :



  • Nuage de points (Wikipédia) et courbe obtenue avec un taux de 8,67% par siècle.

    Graphique 2
    Nuage de points (Wikipédia) et courbe obtenue     avec un taux de 8,67% par siècle.

Comme on peut le remarquer, la courbe rouge obtenue avec un taux de 8,67% par siècle est proche du nuage de points du site Wikipédia.

Grâce au site Internet intitulé notre-planete.info, nous pouvons profiter d'une autre representation graphique de l'évolution de la population mondiale :



  • Courbe d'évolution de la population mondiale de -100000 à 1850.

    Graphique 3
    Courbe d'évolution de la population mondiale de -100000 à 1850.

Cette courbe représentative apparaît moins régulière que la précédente. On y voit des changements de concavité. Elle ressemble à une vraie courbe d'économie avec ses bosses et ses creux. Cependant, les changements de concavité sont trompeurs. En effet, la courbe a été probablement obtenue par la méthode suivante : on a estimé les effectifs de la population mondiale aux années -2000, 400, 1000, 1400, 1500, etc. Et on a relié les points obtenus. sans tenir compte des écarts. Ainsi entre -2000 et 400, l'écart est de 2400 ans , entre 400 et 1000, de 600 ans, entre 1000 et 1400, de 400 ans,..., entre 1800 et 1850, de 50 ans, En prenant des écarts réguliers, on aurait certainement obtenu une courbe analogue à la courbe rouge obtenue précédemment. Notre hypothèse est que les deux courbes ont été obtenues à partir de la même source d'informations. On remarque un changement de trajectoire (mais il n'apparaît pas sur cette courbe) : à partir de 1750, le taux d'accroisement devient nettement plus élevé : c'est l'apparition de l'ère industrielle.

Notre étude devant être effectuée sur l'intervalle temporel [1, 1200], nous pouvons accepter un taux d'accroissement de construction de monuments de 8,67 % (il ne s'agit que d'une valeur approchée).




Annexe 2 concernant la deuxième approche de l'étape 1 : Évaluation en pourcentage de l'effectif des monuments attribuables au premier millénaire de notre ère.

Cette deuxième approche consiste à utiliser les données statistiques établies lors de la rédaction de la page intitulée La « Vérité » extraite des guides touristiques, au tout début des pages de l'onglet  Datation. Ces données concernaient les monuments qui subsistent de ce passé. Nous avons amélioré le graphe réalisé auparavant en utilisant les données statistiques du tableau ci-dessous :



  • Tableau des monuments en Europe.

    Tableau 4
    Tableau des monuments en Europe.

La première ligne est celle des siècles, du premier au quinzième. Les lignes de 2 à 8 founissent les effectifs des monuments par siècle de 7 pays d'Europe issus de la lecture des Guides Verts Michelin. La neuvième ligne, intitulée un peu abusivement Europe, réalise, colonne par colonne, la somme des effectifs de ces pays. Ces résultats écrits sur un fond bleu permettent d'obtenir la courbe bleue du graphe ci-dessous. La dixième ligne intitulée Estimation Europe s'efforce d'établir un modèle utilisant un accroissement constant au cours des siècles. Pour que ce modèle soit cohérent, il faut qu'on puisse le calquer sur le graphe précédent (mêmes points de départ et d'arrivée, partage en deux parties égales des aires constituées par les écarts des courbes). Un taux d'accroissement de 29,9% par siècle a été utilisé pour ce modèle. On obtient la courbe rouge.



  • Courbes (lignes 9 et 10 du tableau 4).

    Graphique 5
    Courbes (lignes 9 et 10 du tableau 4).



Annexe 3 : Proposition d'une datation sous la forme que nous avons appliquée sur ce site (une seule date accompagnée de l'incertitude par rapport à cette date)

Exemple : an 750 avec un écart de 200 ans.

Reprenons la phrase évoquée dans la page précédente : « Entre les années 400 et 970, on construit des nefs à piliers de type R0000 ». Un historien traditionnel traduirait ainsi : « C'est une nef du VIIIe siècle ». Il réduirait donc la date à l'intervalle [700, 800[, oubliant le reste. Une idée élémentaire consiste à déterminer le centre de l'intervalle soit 685, arrondi à 700. (évaluation tous les 25 ans). Puis l'écart par rapport à cette date : 700-400 = 300. On pourrait penser que la date est : « l'an 700 avec un écart de 300 ans ». Cependant, il faut tenir compte de l'idée selon laquelle, plus on se rapproche des extrêmes, plus il y a raréfaction des éléments. Notre idée est de nous rapprocher du modèle de raisonnement adopté pour les séries statistiques obéissant à des lois dites « normales ». Pour ces séries, on définit une moyenne et un écart-type. Et on a le principe suivant : pour ces séries statistiques, les deux tiers des valeurs sont comprises entre la moyenne moins l'écart-type et la moyenne plus l'écart-type. Et plus de 90% des valeurs sont comprises entre la moyenne moins deux fois l'écart-type et la moyenne plus deux fois l'écart-type. En procédant de même, nous proposons dans ce cas particulier d'adopter comme écart, l'écart de la moyenne par rapport aux extrêmes divisé par deux. Ce qui donnerait, au lieu de « l'an 700 avec un écart de 300 ans »,
« l'an 700 avec un écart de 150 ans ». Cela signifierait que les deux tiers de ces édifices ont une date comptrise entre 550 ans et 850 ans.

On obtient donc :

Pour les nefs à piliers de type R0000 : an 700 avec un écart de 150 ans.

Pour les nefs à piliers de type R1010 : an 1000 avec un écart de 25 ans.

Pour les nefs à piliers de type R1110 : an 1050 avec un écart de 25 ans.

Pour les nefs à piliers de type R1111 : an 1075 avec un écart de 25 ans.




Annexe 4 : Proposition d'utilisation de fonctions mathématiques.

Commençons par transformer un taux d'accroissement par siècle en un taux d'accroissement par an.


Soit le taux d'accroissement par siècle sous forme décimale (exemple : si le taux est , on écrit ) et le taux d'accroissement par an.
On a la formule . D'où on déduit :
.

On obtient ainsi, pour un taux de par siècle, un taux de par an, et, pour un taux de par siècle, un taux de 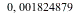par an.

Pour une valeur de , on obtient donc une valeur de . La fonction obtenue associe à une valeur la valeur (exemple : pour la fonction est )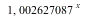

Prenons à présent un groupe d'édifices qui ont été rangés en classes,, dans un ordre chronologique, ( plus ancienne que , laquelle plus ancienne que 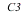…). On a déterminé auparavant les dates extrêmes du groupe entier. Soit 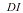la date inférieure, et 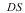la date supérieure. On a aussi déterminé en pourcentages les effectifs des classes ...

La formule permet d'obtenir l'aire comprise entre la courbe d'équation , l'axe des abscisses, et les verticales d'équations et .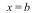

Donc est la valeur de l'aire entre les dates extrêmes. Soit cette aire.

La classe commence à la date et finit à une date inconnue .

On a : 

D'où







On obtient ainsi la valeur de puis, de proche en proche, celles des dates inconnues successives…

On peut même faire mieux que cela ! Rappelons ce que nous avions dit précédemment : on remplace la datation par intervalles (la date est comprise entre deux valeurs 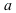et ) par une date centrale de la classe et l'écart par rapport à cette date centrale. Et on avait choisi comme date centrale la moyenne . Ce qui donnait dans un premier temps, la date est avec un écart de (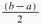, puis dans un second temps, la date est avec un écart de .

Mais dans le cas présent d'une fonction croissante, la valeur moyenne ne correspond pas à la médiane (celle-ci sépare une classe donnée en deux parties d'effectifs égaux).

Par contre dans le cas présent, il est facile de trouver la médiane de chaque partie. Prenons la classe d'effectif . La médiane de cette classe sépare cette classe en deux parties d'effectifs . Il est donc facile d'obtenir sa valeur par la formule






Annexe 5 : loi normale

À la fin de l'annexe 4 de cette page, nous avions présenté un premier modèle effectué à partie des données statistiques suivantes, concernant la répartition de divers types de nef (R0000, R1010, R1110, R1111), entre les années 500 et 1100, avec un taux d'augmentation de 30% par siècle. On avait obtenu les pourcentages suivants : 65% pour R0000, 16% pour R1010, 4% pour R1110, 15% pour R1111.

Nous avions pu créer une partition de l'intervalle temporel en 4 classes successives :
La classe C1 formée de nefs de type R0000 bornée par la date 500 et une date inconnue D1.
La classe C2 formée de nefs de type R1010 bornée par les dates inconnues D1 et D2.
La classe C3 formée de nefs de type R1110 bornée par les dates inconnues D2 et D3.
La classe C4 formée de nefs de type R1111 bornée par la date inconnue D3 et la date 1100.

Grâce aux pourcentages, nous avions montré que l'on pouvait déterminer, non seulement les valeurs inconnues D1, D2 et D3, mais aussi les valeurs des médianes des classes C1, C2, C3 et C4 désignées par Med1, Med2, Med3 et Med4.

En utilisant le logiciel Maple, Alain Le Stang a réalisé un programme pour calculer ces valeurs. En utilisant les données ci-dessus, on obtient :
D1 = 976, D2 = 1038, D3 = 1052 ainsi que : Med1 = 808, Med2 = 1008, Med3 = 1045 , Med4=1077.

La classe C1 correspond à l'intervalle [500, 976], de diamètre 476, de médiane 808,  la classe C2 à l'intervalle [976, 1038], de diamètre 62, de médiane 1008.
La classe C3 correspond à l'intervalle [1038, 1052 ], de diamètre 14, de médiane 1045,  la classe C4 à l'intervalle [1052, 1100], de diamètre 48, de médiane 1077.

Considérons à présent une classe donnée. On peut estimer que le nombre de monuments appartenant à cette classe suit une loi dite normale avec une courbe en cloche dite gaussienne. En fait, ici, ce n'est pas tout à fait une loi normale car la courbe est asymétrique. Dans une loi normale, il y a une moyenne μ et un écart type σ. Pour une loi normale, 68,3% des valeurs sont comprises entre μ – σ et μ + σ et 95,4% des valeurs sont comprises entre μ –2σ et μ +2σ. Pour ce type de loi, la moyenne, la médiane et le mode (pour le plus fort effectif) sont identiques.
La formule de la fonction associée à celle loi est 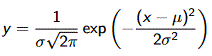. Dans le cas présent, la moyenne et la médiane ne sont pas identiques.



Premiers constats

Le modèle et les méthodes de recherche que nous avons proposés conduisent à l'évaluation suivante :

Pour les nefs à piliers de type R0000 : an 700 avec un écart de 150 ans.

Pour les nefs à piliers de type R1010 : an 1000 avec un écart de 25 ans.

Pour les nefs à piliers de type R1110 : an 1050 avec un écart de 25 ans.

Pour les nefs à piliers de type R1111 : an 1075 avec un écart de 25 ans.

Il faut dire premièrement que la méthode que nous avons abordée ici est de type expérimental ; c'est un test. En conséquence, nous pourrions ne pas attacher d'importance aux résultats et attendre d'avoir fait d'autres tests avec des taux d'accroissement différents (10% par siècle, 20%, 40%, etc.) pour tirer des conclusions. Cependant, nous pensons que d'ores et déjà, ces résultats confirment au moins en partie nos premières observations qui n'étaient basées que sur des impressions à partir de l'analyse de l'architecture. Ainsi, pour les nefs à piliers de type R0000, nous proposions des dates aux alentours de l'an 800 :  « an 800 avec un écart de 200 ans », ou
« an 750 avec un écart de 200 ans ». Bien sûr, il existe une différence non négligeable (100 ans !) entre ces deux évaluations. Mais cela change radicalement avec l'opinion couramment admise que tout est du XIIe siècle.