Autres tests. Difficultés à définir une modélisation
• Essais
de datation • Article
précédent • Article
suivant
À la fin de la page précédente intitulée Essai
de datation des nefs à trois vaisseaux : les méthodes,
page d'annexes, nous avions obtenu le résultat
suivant pour les nefs de différents types. Pour les nefs à
piliers de type R0000
: an 700 avec un écart de 150 ans ; de type R1010
: an 1000 avec un écart de 25 ans ; de type R1110
: an 1050 avec un écart de 25 ans ; de type
R1111 : an 1075 avec un écart de 25 ans.
Ce partage ayant été effectué aux débuts de la création du site, nous n'avions pas vu l'ampleur qu'il aurait (pour mémoire : nous sommes partis de 500 monuments non encore étudiés, dont une bonne partie présumés postérieurs à l'an 1000, à plus de 2500 édifices étudiés). En particulier, nous n'avions pas prévu le nombre plus important d'édifices de type R0000. Au fur et à mesure, notre réflexion a évolué et nous avons envisagé que certains édifices de type R0000 pouvaient être postérieurs à l'an 800.
Cependant, nous n'avions pas prévu que la date de ce type de nef serait comprise entre les années 500 et 970, soit un écart de près de 500 ans entre les dates extrêmes. Cet écart trop grand nous oblige à repenser l'étude de ce type de nef qui a dû suivre une évolution au cours du temps, une évolution dont il faut rechercher les signes. Mais il faut aussi regarder à l'autre bout de la liste, du côté des dates entre 970 et 1100. On découvre que dans un intervalle de temps très court, trois innovations importantes ont été faites :en 1000, 1050, 1075. Il nous semble que c'est trop court. D'autant que ces innovations apparemment très anodines sont liées à d'autres innovations plus significatives : voûtes en plein cintre sur doubleaux, voûtes d'arêtes, croisées d'ogives. En conséquence, il devient non seulement nécessaire de constituer une ou plusieurs listes contenant un échantillon relativement réduit de monuments (100 à 200), mais aussi de réétudier chacun de ces monuments afin d'être en mesure d'affiner les datations.
Une autre difficulté est liée à l'évaluation des écarts par rapport à la médiane. Comme nous l'avons écrit dans la page précédente, nous associons la répartition des monuments d'une classe donnée à une loi dite normale ou gaussienne d'équation
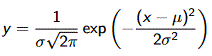 , où μ
est la moyenne et σ l'écart-type.
, où μ
est la moyenne et σ l'écart-type. La courbe représentative de cette fonction est une courbe en cloche.
Mais à quoi peut servir de calculer la moyenne et l'écart-type ? Pour la moyenne, on le comprend assez bien. Pour l'écart-type, c'est un peu plus compliqué. Les graphiques ci-dessous fournissent une explication. Pour une loi normale, 68,3% des valeurs sont comprises entre μ - σ et μ + σ (graphique 1), et 95,4% des valeurs sont comprises entre μ - 2 σ et μ + 2 σ (graphique 2). Il est donc important d'avoir une connaissance relativement précise d'un écart-type. À tire de comparaison, c'est ce qui se passe en ce qui concerne les sondages électoraux : il ne sert à rien de dire qu'un candidat, tributaire de 35 points, devrait l'emporter sur un autre qui en a 33, si l'écart estimé sur chacun est de 5.
Nous avons cependant pensé que l'on pouvait trouver un ajustement entre les deux informations : celle évoquée dans l'annexe 3 et l'annexe 4 de la page préédente, utilisant les pourcentages d'édifices d'un type donné, permettant un encadrement entre deux dates de ce type d'église, et celle évoquée ci-dessus. En fait, pour la première on encadre une classe Ci entre deux dates, di-1 et di. Le diamètre de cette classe est Diami = di- di-1. Or si l'on utilise la seconde information donnée ci-dessus, il y a 95,4 % de chances pour que le diamètre corresponde à 4σi.
Notre idée première a donc été de prendre pour σi la valeur Diami /4. On peut donc penser qu'il y a plus de 95 chances sur 100 que les valeurs soient comprises entre les bornes μi - 2σi et μi + 2σi .
La courbe représentative fi d'une classe Ci est une courbe en cloche. Mais elle est asymétrique, car il faut tenir compte du fait que le sommet de la courbe (valeur maximum) est situé non pour la moyenne, mais pour la médiane.
Nous avons tenté dans une première approche de définir fi(x) comme produit par (1+t)x de la valeur en x de la loi gaussienne, c'est à dire par une expression de la forme
y = fi (x) = Ki . exp ( - (x - μi)²/(2 σi²) . (1+t)x. Mais les simulations réalisées par Alain Le Stang en utilisant le logiciel Maple se sont avérées très décevantes. Malgré ces tâtonnements, on a pu progresser, pour aboutir à une expression beaucoup plus satisfaisante. C'est souvent ainsi que la science avance !
Cette expression de la fonction fi associée à cette courbe sur [di-1 , di] est de la forme :
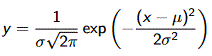 que l'on multipliera par un coefficient Ki bien choisi.
Dans la littérature mathématique, on parle de l'expression de y
comme d'un noyau
gaussieni.
que l'on multipliera par un coefficient Ki bien choisi.
Dans la littérature mathématique, on parle de l'expression de y
comme d'un noyau
gaussieni.La valeur T (taux d'augmentation par siècle) est donnée dès l'origine. On en déduit t (taux d'augmentation par an). Les valeurs de μ et σ viennent d'être données. Il reste à calculer la valeur de Ki.
En résumé : La courbe en cloche pour la classe Ci aura pour équation y = fi (x) = Ki exp ( - (x - μi )²/(2 σi ²) avec μi = Medi et σi = Diami/4 = (di - di-1)/4.
L'idée alors est de tracer les deux courbes, celle de la fonction croissante et celle de la courbe en cloche représentative de Ci sur un même graphique, avec des couleurs différentes. Puis après tracer la courbe de la fonction croissante et toutes les courbes en cloche associées aux classes C1, C2, ... ,Cn.
L'idée finale est de tracer la courbe de la fonction croissante et la courbe de la somme des fonctions f1+f2 +...+fn.
Nouveaux tests. Autres déceptions
Après des premiers tests un peu décevants, nous avons estimé qu'il était nécessaire de prendre en compte des constructions estimées comme romanes (donc postérieures à l'an mille). En effet, l'étude que nous avions faites portait sur les nefs triples à piliers rectangulaires. Or, au cours du premier millénaire, on n'avait pas construit que des nefs triples à piliers rectangulaires. On avait pu construire des églises à nef unique, des nefs triples à piliers cylindriques, des transepts, de nouveaux chevets. Nous avons donc décidé de reprendre les expériences à partir du même échantillon de 161 monuments. Mais en prenant cette fois-ci 5 classes :
C1 : nefs à piliers R0000 ou C0000 ou M0000.
C1 : nefs à piliers R1010 ou M1010.
C3 : nefs à piliers R1110.
C4 : nefs à piliers R1010 ou (M0000 et galeries supérieures).
C5 : parties romanes (voûtes, transepts, ouvrage Ouest, …).
Nous avons choisi pour taux d'augmentation 30% par siècle et pour bornes de l'intervalle d'étude 500 et 1150.
Le graphique 3 représente la simulation effectuée par Alain Le Stang en utilisant le logiciel Maple, avec Ki = g(di)/f(μi) et les données :
T = 30, DI = 500, DS = 1150, n = 5, [e1,e2,e3,e4,e5] = [35,13.5,3,8,40.5], σi = Diami/4.
On peut y lire, dans les 5 premiers cadres, le graphique rassemblant les deux courbes, celle de la fonction croissante, g, et celle de la fonction fi, de la courbe en cloche associée à la classe Ci, avec des couleurs différentes : g(x)=(1+t)x en rouge, fi(x) = Ki exp ( - (x - μi )²/(2 σi ²) en bleu, la portion en gras correspondant à l'intervalle restreint
[di-1 , di]. La fonction représentée dans le dernier cadre est la somme des fonctions gaussiennes f1+f2 +...+fn en violet.
La divergence des courbes aux bornes des intervalles
Il est tout à fait normal que les deux courbes se détachent aux extrêmes, la courbe de la somme des fonctions se rapprochant de l'horizontale. Cela vient du fait que nous n'avons pas pris en compte les constructions antérieures (romaines) et postérieures (gothiques). Tout comme l'an 2000 dont nous avons vécu le passage, les années 400 et 1150 ne doivent pas être conçues comme des années de grands bouleversements, de changements de systèmes. Les changements se sont effectués progressivement, parfois sans que ceux qui les ont vécus en prennent conscience, hormis les sempiternels regrets : « Autrefois, c'était le bon temps ! ». Si, avant l'an 400, on a construit des monuments romains, on a continué à construire, soit sur des monuments romains, soit de nouveaux monuments de même style que les romains, après l'an 400, en même temps qu'apparaissaient des constructions d'un nouveau style. De même, l'architecture romane a été au fur et à mesure remplacée par l'architecture gothique vers l'an 1150. Mais longtemps après l'an 1200, on a continué à construire dans le roman, tout en connaissant les propriétés caractéristiques de l'architecture gothique (exemple : le style néoroman).
Il serait donc nécessaire de mieux encadrer la distribution en indiquant les courbes associées aux monuments romains et aux monuments gothiques. C'est cependant difficile à réaliser dans le cadre de l'étude que nous avons faite. Lorsque nous avons démarré notre site, nous avons écarté d'emblée l'étude des monuments romains, estimant, à tort, que cette étude avait été faite auparavant et qu'il n'était pas nécessaire de la reprendre. De même, nous pensions qu'il était inutile de reprendre l'étude des monuments postérieurs à l'an 1100. En conséquence, l'inventaire exhaustif des monuments antérieurs à l'an 400 et postérieurs à l'an 1100 n'a pas été entrepris. Il faudra cependant effectuer une estimation des bornes : fin du romain, début du gothique.
Les pics de fluctuation
Revenons au graphique 3. Si la pente de la courbe représentative de la fonction g apparaît faible et régulière sur l'intervalle [400, 1150], il n'en est pas de même des pentes des courbes représentatives des fonctions f2, f3, f4. Le résultat obtenu pour la courbe de la somme des fonctions est très différent de celui de la courbe g avec des fluctuations beaucoup trop importantes. Est-il possible que nous nous soyons trompés ? Pourtant, nous n'avons pas a priori fait d'erreur. Tout semble en accord avec la théorie des fonctions gaussiennes. Mais il ne faut pas oublier un point qui a priori semble être de détail. Nous avons basé toute notre étude sur les hypothèses suivantes : un taux d'accroissement de 30% par siècle, un intervalle d'étude [500, 1150], une partition en 5 classes d'effectifs respectifs 35, 13.5, 3, 8, 40.5 (en pourcentages). Si on change un seul de ces paramètres, on modifie les résultats. C'est ce que nous avons essayé de faire avec la valeur 400.
Dans le tableau 4 ci-dessous, la première ligne correspond à la situation modélisée ci-dessus. Pour la deuxième ligne, on a remplacé la valeur 500 par 400. Parmi les colonnes du tableau donnant les résultats, nous n'avons conservé que celles relatives aux classes C1 et C2. Les valeurs des colonnes intitulées Diam C1 et Diam C2 définissent dans chaque cas les valeurs de 4σ1 et de 4σ2. En conséquence, si on suit la loi normale, les intervalles de confiance obtenus en retranchant ou en ajoutant la valeur de 2σi à la médiane doivent normalement contenir 95,4% des effectifs.
Nous devons conclure de cette petite expérience que l'écart par rapport à la médiane doit être réexaminé. En effet la valeur de σ correspond à l'écart-type. D'après la loi normale, plus de 95% des valeurs sont comprises entre μ - 2 σ et μ + 2 σ. Dans le cas de la classe C3, en prenant une médiane, l'autre est extérieure à l'intervalle de confiance avec une probabilité supérieure à 95%. Et ce pour une modification relativement négligeable compte tenu des approximations que nous faisons : 400 au lieu de 500.
On a amélioré les résultats du graphique 3 en multipliant chaque noyau gaussien par un coefficient Ki , les Ki étant calculés pour que la somme des Ki.fi(μi), pour i allant de 1 à n = 5, égale g(μi), avec g(x) = (1+t)x sur l'intervalle [di-1 , di].
C'est ce que l'on constate sur le graphique 5 ci-dessous, pour les valeurs de σi, respectivement σi = (di - di-1)/4, σi= (di - di-1)/3, σi = (di - di-1)/2, de gauche à droite.
La présence du coefficient
Nous le constatons sur le graphique 6, où l'on voit le résultat de la simulation obtenue par Maple en programmant ce modèle, avec les mêmes données que pour le graphique 5 et σi = (di - di-1)/3. En comparant avec le résultat du cadre au centre du graphique 5, on a une meilleure approximation de g.
Nouvelle idée : moduler la valeur de σi en fonction du diamètre (di - di-1) de la classe Ci.
Nous avons choisi σi = (di - di-1)/4, que nous conserverons pour un grand diamètre, comme celui de C1.
Pour un diamètre moyen comme celui de C5, prendre par exemple σi = (di - di-1)/3.
Pour un diamètre petit comme celui de C2, prendre par exemple σi = (di - di-1)/2.
Pour un diamètre très petit, comme celui de C3 et C4, prendre par exemple σi = (di - di-1).
En augmentant ainsi la valeur de σi, on obtient des courbes aux pentes moins accentuées, de formes plus évasées. En compensation, les amplitudes sont moins fortes.
On améliore ainsi les résultats du graphique 3. C'est ce que l'on constate sur le graphique 7 ci-dessous, pour les valeurs de σi, respectivement σ1 = (d1- d0)/4,
σ2 = (d2 - d1)/2, σ3 = (d3 - d2), σ4 = (d4 - d3) et σ5 = (d5 - d4)/3.
Pour un grand effectif comme celui de C1 et C5, prendre par exemple σi = (di - di-1)/2.
Pour un effectif moyen comme celui de C2, prendre par exemple σi = (di - di-1).
Pour un effectif petit comme celui de C4, prendre par exemple σi = 2 (di - di-1).
Pour un effectif très petit comme celui de C3, prendre par exemple σi = 4 (di - di-1).
On améliore ainsi les résultats du graphique 7. C'est ce que l'on constate sur le graphique 8 ci-dessous, pour les valeurs de σi, respectivement σ1 = (d1- d0)/2,
σ2 = (d2 - d1), σ3 = 4 (d3 - d2), σ4 = 2 (d4 - d3) et σ5 = (d5 - d4)/2.
Conséquences de cette recherche en datation
Conséquence 1 : Abandon d'une datation au siècle
Cette recherche nous a conduit à une remise en question de notre mode de raisonnement en matière de datation. Un mode de raisonnement qui n'est pas seulement le nôtre,mais celui de toute la communauté des historiens et, par transfert, de la communauté des humains. Nous raisonnons en termes de siècles. Dès la Renaissance italienne, ont été définies des périodes comme le Trecento (XIVe Siècle) ou le Quattrocento (XVe Siècle). Ces périodes apparaissaient étanches et cloisonnées. Ainsi, un peintre du Trecento ne pouvait pas aussi faire partie du Quattrocento alors qu'il pouvait avoir vécu sur les deux périodes. Et consciemment ou non, la grande majorité des chercheurs avaient intégré le système. C'est en tout cas ce que nous avons constaté en ce qui concerne la datation des monuments. Comme l'art roman était défini comme étant du XIe ou du XIIe siècle, une église romane ne pouvait pas être antérieure à l'an mille. Et ce, même si un document mentionnait son existence en l'an 980.
Notre recherche nous a amené à utiliser des fonctions gaussiennes, à employer des termes comme moyenne et écart-type. Montrons ici la différence entre les deux conceptions. Dans la conception traditionnelle, le XIIe siècle correspond à l'intervalle temporel fixé [1100, 1199 ]. Dans la nouvelle conception, on peut parler de l'an 1150 avec un écart de 50 ans. Cela semble la même chose mais c'est différent dans la mesure où l'on peut envisager un franchissement des bornes 1100 ou 1199 : ces bornes ne sont pas rigides. En fait, l'idéal serait de donner les informations sous la forme : an 1150 avec un écart-type de 25 ans. Mais il faudrait être en présence d'un public averti qui connaît la loi normale et interprète ainsi l'information : il y a plus de 68% de chances que la date soit comprise entre 1125 et 1175, et plus de 95% de chances qu'elle soit comprise entre 1100 et 1200. Nous n'en sommes pas encore là !
Cependant, cette façon de procéder peut permettre de mieux centrer l'information. Ainsi, il nous est arrivé de rencontrer des datations telles que, « église du XIIe siècle »,
« église de la première moitié du XIIe siècle », « église du deuxième quart du XIIe siècle », donnant l'impression d'une plus grande précision avec des intervalles de confiance de 100 ans pour la première, de 50 ans pour la seconde, et de 25 ans pour la troisième. Une plus grande précision qui s'avère, en absence de preuves solides, parfaitement ridicule dans le troisième cas (on a tendance à dire dans ce cas : « qu'il commence par dater avec une telle précision les immeubles du XIXe ou XXe siècle de la ville voisine ! »). Il est cependant possible que l'évaluateur ait estimé que dans le premier cas, la date devait être aux alentours de 1150, dans le second cas de 1125, et dans le troisième cas de 1137. En utilisant pour chacune des dates le même écart, par exemple 50 ans, l'évaluateur peut sans problème éviter l'écueil évoqué ci-dessus en donnant comme datation dans le premier cas « an 1150 avec un écart de 50 ans », dans le second cas « an 1125 avec un écart de 50 ans », et dans le troisième cas « an 1137 avec un écart de 50 ans ».
Conséquence 2 : Adoption d'une datation centrée au quart de siècle (pour les monuments du premier millénaire)
En histoire ancienne, la datation d'un événement est en général très imprécise. C'est déjà vrai dans le cas de la vie de personnages célèbres (quelle est la date de naissance de Jésus-Christ ?). Ce l'est encore plus en ce qui concerne les constructions. À cela s'ajoute le fait qu'une construction s'étale dans le temps, entre l'élaboration du projet et l'inauguration du bâtiment. En conséquence, la datation d'une construction au jour près ou même au mois près n'a aucune signification, et ce, même si on dispose de documents écrits mentionnant la date exacte au jour près d'un événement, comme la pose de la première pierre ou l'inauguration du bâtiment ; plusieurs années peuvent s'écouler entre ces deux moments.
Et, dans le cas le plus général, on ne dispose d'aucun document écrit. On ne peut dater le monument que par son style, en le comparant à d'autres monuments qui sont eux datés. Dans ces conditions, une datation à l'année est non seulement inutile, mais nuisible, dans la mesure où elle empêche une vision d'ensemble. C'est pour cela que nous envisageons une datation au quart de siècle, tant pour la date que pour l'incertitude par rapport à cete date. Ainsi, en ce qui concerne la série précédente, on donnera pour la classe :
C1 (de médiane = 722 et diamètre/2 = 180) : an 725 avec un écart de 175 ans.
C2 (de médiane = 903 et diamètre/2 = 40) : an 900 avec un écart de 50 ans.
C3 (de médiane = 950 et diamètre/2 = 8) : an 950 avec un écart de 25 ans.
C4 (de médiane = 978 et diamètre/2 = 20) : an 975 avec un écart de 25 ans.
C5 (de médiane = 1083 et diamètre/2 = 76) : an 1075 avec un écart de 75 ans.
En fait, compte tenu de ce qui a été écrit précédemment, il est préférable de prendre des écarts plus importants pour C2, C3 et C4 : au moins 50, voire même 75.
Conséquence 3 : Adoption d'une classification en groupes et sous-groupes
Notre recherche en datation a débuté par l'essai d'identification de marqueurs chronologiques. Nous en avons trouvé en ce qui concerne les églises à nefs triples et piliers rectangulaires et nous avons petit à petit envisagé la chronologie (R0000, R1010, R1110, R1111) permettant de classer ces églises. Mais, toujours petit à petit, nous avons réalisé que ce type de classification n'était pas transposable aux édifices à piliers cylindriques (presque tous de type C0000) ou aux nefs uniques. C'est-à-dire à la totalité des constructions. Nous nous sommes aussi aperçus que, concernant les nefs à piliers rectangulaires, les séries n'étaient pas équilibrées : il y a beaucoup plus de nefs à piliers R0000 que de nefs à piliers R1110. Et ce déséquilibre a été source des difficultés signalées ci-dessus.
Nous pensons qu'il faut en revenir à l'exemple qui nous est donné par l'analyse stratigraphique géologique. Nous avons appris sur les banc scolaires qu'il y avait quatre périodes géologiques : le primaire, le secondaire, le tertiaire et le quaternaire. Plus tard, nous avons appris que chacune de ces périodes pouvait être divisée en plusieurs sous-périodes. Ainsi, pour le secondaire : le trias, le jurassique et le crétacé. Et on peut encore faire des sous-périodes de sous-périodes. Ainsi pour le Crétacé, le Crétacé Supérieur et le Crétacé Inférieur. Et à l'intérieur du Crétacé Supérieur, on a encore six sous-périodes : le Maastrichien, le Campanien, le Santonien, la Coniacien, le Turonien, le Cénomanien. Et ainsi de suite.
Nous envisageons donc d'orienter la réflexion dans ce sens en commençant par partager la période [1, 1200] en quatre parties : le romain, le romain tardif, le préroman, le roman. Puis une fois cela réalisé, essayer de partager chacune de ces parties en trois ou quatre sous-groupes.